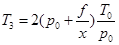圆柱形气缸筒长2l,截面积为S,缸内有活塞,活塞可以沿缸壁无摩擦不漏气的滑动,气缸置于水平面上,缸筒内有压强为p0,温度为T0的理想气体,气体体积恰好占缸筒容积的一半,如图所示。此时大气压也是p0,弹簧的劲度系数为k,气缸与地面的最大静摩擦力为f,求:
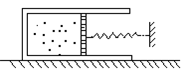
(1)当kl<f,对气缸缓慢加热到活塞移至缸筒口时,气缸内气体温度是多少?
(2)当kl>f,对气缸缓慢加热到活塞移至缸筒口时,气缸内气体的温度又是多少?
见解析
【错解分析】错解:(1)以整体为对象。∵kl<f,所以在活塞移至缸口时(此时弹簧弹力为kl),系统始终静止。
以活塞为对象,末态受力如图所示。
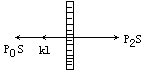
由平衡条件可知:p2S=p0S+kl
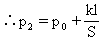
以气体为对象,p1=p0 V1=ls T1=T0
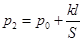
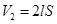
由理想气体状态方程: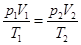
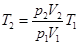
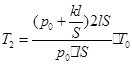
解得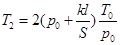
(2)当kl>f时,气缸要滑动
解法一:与(1)解法类似
对活塞受力分析如图所示
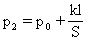
其余解法与(1)相同,答案也与(1)相同,说明两种情况没有区别。
解法二:以活塞为对象受力分析如图
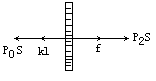
p2S+f=kl+p0S
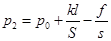
对气体应用气态方程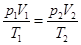
有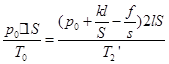
解得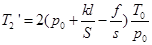
【错解原因】此题第一问解法及答案均正确。错误主要发生在第二问:(1)没有详细地分析kl>f情况下气缸,活塞的运动,而是套用了第一问解题的思路,分不清kl<f与kl>f在此题中的本质区别。(2)解法2对活塞受力分析出现了气缸受力f,导致错误。
【正解】第一问如上所述,略。
第二问,当kl>f,就意味着弹簧压缩到一定程度,设压缩量为x,即kx=f处,就不继续压缩,这之后,气缸开始滑动,而气体则做等压升温膨胀。
气体的变化可以分为三种状态两个过程,如图8所示。
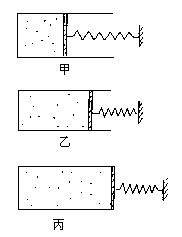
第一个过程:甲态→乙态,p,V,T都变。
在乙态对活塞受力分析可确定此时气体的压强为: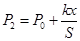
而丙态的压强与乙态相同,
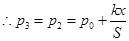 其中
其中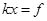
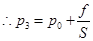
第二个过程:从甲态→丙态应用气态方程
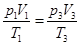 代入数据
代入数据
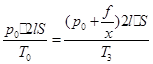
解得