问题
解答题
函数f(x)的定义域为D={x|x≠0},且满足对于任意x1、x2∈D,
有f(x1● x2)=f(x1)+f(x2).
(1)求f(1)的值;
(2)判断f(x)的奇偶性并证明;
(3)如果f(4)=1,f(3x+1)+f(2x﹣6)≤3,且f(x)在(0,+∞)上是增函数,求x的取值范围.
答案
(1)解:令x1=x2=1,有f(1×1)=f(1)+f(1),解得f(1)=0.
(2)证明:令x1=x2=﹣1,有f[(﹣1)×(﹣1)]=f(﹣1)+f(﹣1).解得f(﹣1)=0.
令x1=﹣1,x2=x,有f(﹣x)=f(﹣1)+f(x),
∴f(﹣x)=f(x).
∴f(x)为偶函数.
(3)解:f(4×4)=f(4)+f(4)=2,f(16×4)=f(16)+f(4)=3.
∴f(3x+1)+f(2x﹣6)≤3即f[(3x+1)(2x﹣6)]≤f(64).(*)
∵f(x)在(0,+∞)上是增函数,
∴(*)等价于不等式组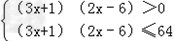 或
或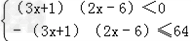
或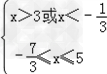 或
或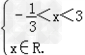
∴3<x≤5或﹣ ≤x<﹣
≤x<﹣ 或﹣
或﹣ <x<3.
<x<3.
∴x的取值范围为{x|﹣ ≤x<﹣
≤x<﹣ 或﹣
或﹣ <x<3或3<x≤5}.
<x<3或3<x≤5}.
