问题
问答题
一质量为10kg的木楔ABC静止在粗糙的水平面上，物块与斜面动摩擦因素为0.2，在倾角为θ=37°的木楔斜面上，有一质量为1kg的物块，以初速度为v=7.6m/s开始沿斜面上滑，在这一过程中，木楔始终处于静止状态．（取g=10m/s2，sin37°=0.6，cos37°=0.8），求：
（1）物块在斜面上运动时的加速度a；
（2）物块上升到最高点所需的时间t；
（3）在物块向上运动时地面给木楔的摩擦力f和支持力N各是多少．
答案
（1）物块沿斜面向上滑动的过程中，受到重力、斜面的支持力和沿斜面向下的滑动摩擦力．
根据牛顿第二定律得：
mgsinθ+μmgcosθ=ma ①
得a=g（sinθ+μcosθ）=10（0.6+0.2×0.8）=7.6m/s2
（2）由v=v0-at=0得，物块上升到最高点所需的时间 t=
=1s v0 a
（3）对斜面体受力分析（如图所示）并建立坐标系，在X方向上：
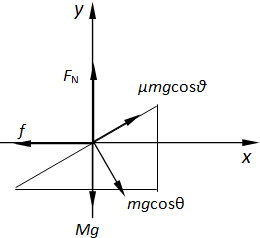
f=（μmgcosθ）cosθ+（mgcosθ）sinθ ②
N+（μmgcosθ）sinθ=Mg+mgcosθ•cosθ ③
由①②得f=macosθ=10×7.6×0.8N=6.08N
由①③得N=（M+m）g-masinθ=105.44N
答：
（1）物块在斜面上运动时的加速度a；
（2）物块上升到最高点所需的时间t；
（3）在物块向上运动时地面给木楔的摩擦力f和支持力N各是6.08N和105.44N．
C(g)+D（g)的化学平衡常数和温度的关系如下：