问题
问答题
如甲图所示,传送带与水平方向夹角θ=30°长度很长.传送带正在做加速度a0=5m/s2的匀减速运动直至静止,运动方向为逆时针转动.在t=0时刻,传送带的速度v0=17.5m/s,恰在此时A端无初速度的释放一个m=1kg的黑色煤块,已知煤块与传送带之间的动摩擦因数μ=
取g=10m/s2.3 2 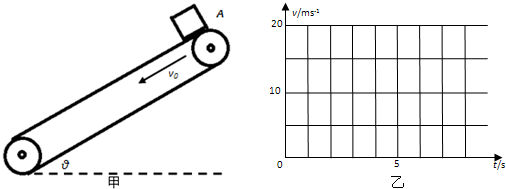
(1)求t=0时刻,煤块运动的加速度大小a1
(2)试在乙图中画出传送带(用虚线)速度随时间变化的图象
(3)试在乙图中画出煤块(用实线)速度随时间变化的图象.
答案
(1)t=0时刻,物体相对于皮带向上运动,所以受到沿斜面向下的滑动摩擦力,根据牛顿第二定律:
ma1=mgsinθ+μmgcosθ
得:a1=12.5m/s2
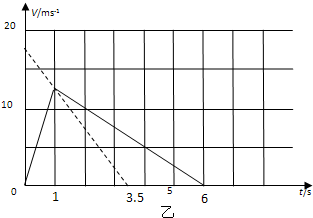
(2)煤块做匀减速直线运动,加速度a0=5m/s2,如图中虚线所示;
(3)当煤块速度与传送带速度相等后之后,由于煤块速度大于传送带速度,所以受向后的摩擦力,根据牛顿第二定律:
mgsinθ-μmgcosθ=ma2,得:a2=-2.5m/s2
故煤块全过程的速度图象如图中实线所示;
答:(1)t=0时刻,煤块运动的加速度大小a1为12.5 m/s2;
(2)如图中虚线;
(3)如图中实线.
