如图所示，A球运动到最低点时速度为V₀，A球受到向下重力mg和细管向上弹力N₁的作用，其合力提供向心力．根据牛顿第二定律，得N₁-m₁g=m₁

v 20

R

①

这时B球位于最高点，设速度为V₁，B球受向下重力m₂g和细管弹力N₂作用．球作用于细管的力是N₁、N₂的反作用力，要求两球作用于细管的合力为零，即要求N₂与N₁等值反向，N₁=N₂ ②，且N₂方向一定向下，

对B球：N₂+m₂g=m₂

v 21

R

③B球由最高点运动到最低点时速度为V₀，此过程中机械能守恒定律，得：

即

1

2

m₂V₁²+m₂g•2R=

1

2

m₂V₀² ④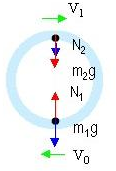

由①②③④式消去N₁、N₂和V₁后得到m₁、m₂、R与V₀满足的关系式是：

（m₁-m₂）

v 20

R

+（m₁+5m₂）g=0 ⑤

答：m₁、m₂、R与v₀应满足的关系式为 （m₁-m₂）

v 20

R

+（m₁+5m₂）g=0