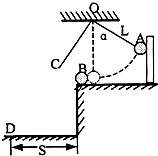
某同学用如图所示装置验证动量守恒定律,用轻质细线将小球1悬挂于O点,使小球1的质心到悬点O的距离为L,被碰小球2放在光滑的水平桌面上.将小球1从右方的A点(OA与竖直方向的夹角为α)由静止释放,摆到最低点时恰与小球2发生正碰,碰撞后,小球1继续向左运动把轻质指示针推移到图中的OC位置,小球2落到水平地面上到桌面边缘水平距离为S的D点.
(1)实验中已经测得上述物理量中的α、L、S,为了验证两球碰撞过程动量守恒,还应该测量物理量有______.
(2)请用测得的物理量结合已知物理量来表示碰撞前后小球1、小球2的动量:P1=______.P′1=______.P2=______.P′2=______.
(1)为了验证两球碰撞过程动量守恒,需要测量两小球的质量,小球1质量m1,小球2质量m2,小球1碰撞前后的速度可以根据机械能守恒定律测出,所以还需要测量OC与OB夹角,需要通过平抛运动测量出小球2碰后的速度,需要测量水平位移S和桌面的高度h.
(2)小球从A处下摆过程只有重力做功,机械能守恒,由机械能守恒定律得:
m1gL(1-cosα)=
m1v12,解得v1=1 2
.则P1=m12gL(1-cosα)
.2gL(1-cosα)
小球A与小球B碰撞后继续运动,在A碰后到达最左端过程中,机械能再次守恒,
由机械能守恒定律得:-m1gL(1-cosβ)=0-
mv1′2,解得v1′=1 2
,则P1′=m12gL(1-cosθ)
.2gL(1-cosθ)
碰前小球B静止,则PB=0;
碰撞后B球做平抛运动,水平方向:S=v2′t,竖直方向h=
gt2,联立解得v2′=s•1 2
,则碰后B球的动量P2′=m2s•g 2h
.g 2h
故答案为:(1)小球1质量m1,小球2质量m2,桌面高度h,OC与OB夹角
(2)P1=m
P′1=m12gL(1-cosα)
.2gL(1-cosθ)
P2=0 P′2=m2s•g 2h
