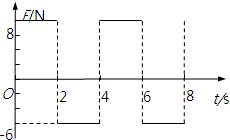
一个质量为2kg的物体静止在足够大的水平地面上,物体与地面间的动摩擦因数μ=0.2.从t=0开始,物体受到一个大小和方向呈周期性变化的水平力F的作用,力F随时间的变化规律如图所示.重力加速度g=10m/s2,
求:
(1)0~2s时间内物块运动的加速度a1的大小和方向;
(2)t=2s时物块运动的瞬时速度v1的大小和方向;
(3)0~6s时间内物块运动的位移的大小和方向.
(1)据牛顿第二定律知:F-μmg=ma1
a1=
=2m/s28-0.2×2×10 2
加速度a1的方向向右.
(2)据速度公式有:v1=a1t1=2×2=4m/s
速度v1的方向向右.
(3)0~2s时间内物块运动的位移为
x1=
a1t12=1 2
×2×22=4(m),方向向右;1 2
2~4s时间内,物块先向右匀减速运动至速度为零,令加速度a2,用时t2;
据牛顿第二定律有:a2=
=F+μmg m
=5m/s2,方向向左 6+0.2×2×10 2
据速度公式有:0=v1+a2t2
t2=
=0-v1 a2
=0.8(s)0-4 -5
物体向右匀减速运动的位移:
x2=v1t2+
a2t22=4×0.8+1 2
×(-5)×0.82=1.6(m)1 2
2.8~4s时间内物块将向左静止开始匀加速运动,令加速度为a3,据牛顿第二定律有:a3=
=F-μmg m
=1m/s2,方向向左;6-0.2×2×10 2
物体向左静止开始匀加速运动的位移:x3=
a3t32=1 2
×(-1)×1.22=-0.72(m),1 2
4s时物体的速度:v3=a3t3=-1×1.2=-1.2(m/s),向左
4~6s时间内物块先向左匀减速运动,令加速度为a4,据牛顿第二定律知:a4=6m/s2
令向左匀减速到静止所用时间为t4,据速度公式有:
0=v3+a4t4
解得:t4=
=0-v3 a4
=0.2(s)0-(-1.2) 6
向左匀减速运动的位移:x4=
t4=v3+0 2
×0.2=-0.12(m)之后,4.2s~6s时间内物块从静止开始向右匀加速运动,-1.2+0 2
加速度a5=a1=2m/s2
向右运动的位移:x5=
a5t52=1 2
×2×1.82=3.24(m)1 2
0~6s时间内的总位移:x=x1+x2+x3+x4+x5=4.0+1.6+(-0.72)+(-0.12)+3.24=8.0(m)
方向向右.
答:(1)0~2s时间内物块运动的加速度2m/s2方向向右. (2)t=2s时物块运动的瞬时速度大小4m/s方向向右.(3)0~6s时间内物块运动的位移的大小8.0(m)方向向右.
