问题
问答题
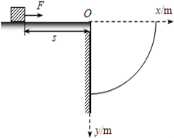
如图所示,在粗糙水平台阶上静止放置一质量m=1.0kg的小物块,它与水平台阶表面的动摩擦因数μ=0.25,且与台阶边缘O点的距离s=5m.在台阶右侧固定了一个
圆弧挡板,圆弧半径R=51 4
m,今以O点为原点建立平面直角坐标系.现用F=5N的水平恒力拉动小物块,小物块在水平台阶上运动一段时间后撤去拉力(已知重力加速度g=10m/s2).2
(1)为使小物块不能击中挡板,求拉力F作用的最长时间;
(2)若小物块在水平台阶上运动时,水平恒力一直作用在小物块上,求小物块击中挡板上的位置坐标.
答案
(1)为使小物块不会击中挡板,拉力F作用最长时间t时,小物块刚好运动到O点.
由牛顿第二定律得:F-μmg=ma1
解得:a1=
-μg=F m
-0.25×10=2.5m/s25 1
减速运动时的加速度大小为:a2=μg=0.25×10=2.5m/s2
由运动学公式得:s=
a12+1 2
a2t221 2
而a1t=a2t2
解得:t=t2=
s2
(2)水平恒力一直作用在小物块上,由运动学公式有:v02=2a1s
解得小物块到达O点时的速度为:v0=
=2a1s
m/s=5m/s2×2.5×5
小物块过O点后做平抛运动.水平方向:x=v0t
竖直方向:y=
gt21 2
又 x2+y2=R2
解得位置坐标为:x=5m,y=5m
答:(1)拉力F作用的最长时间为
s;2
(2)小物块击中挡板上的位置的坐标为x=5m,y=5m.
