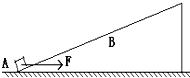
如图所示,倾角θ=37°的斜面足够长,质量m=1kg的滑块静置在斜面的底端A点,滑块与斜面间的动摩擦因素为μ=0.5.现给滑块一个沿斜面向上v°=10m/s的初速度,同时用水平恒力F向右推,使滑块做匀加速运动,在2s后撤去推力F,滑块再运动3s时经过B点,已知AB间距x0=49m,(已知sin37°=0.6,cos37°=0.8).求:
(1)刚撤去推力F时滑块的加速度大小;
(2)推力F的大小.
(1)刚撤去F后,根据牛顿第二定律得,
mgsin37°+μmgcos37°=ma2.
代入数据,解得a2=10m/s2.
(2)在头2s内,滑块的位移x1>v0t1=10×2m=20m.
后3s内,若始终向上减速运动,则x2>
a2t22=1 2
×10×32m=45m.1 2
则x1+x2=65m>49m,故后3s内滑块必定已经沿斜面向上运动到最高点后返回向下运动一段时间.
Fcos37°-mgsin37°-μ(mgcos37°+Fsin37°)=ma1.
解得a1=0.5F-10.
x1=v0t1+
a1t121 2
得x1=20+2a1
v1=v0+a1t1
得,v1=10+2a1
x2=
,将v1=10+2a1代入v12 2a2
解得x2=
.(10+2a1)2 20
t2=
,将v1=10+2a1和a2=10m/s2代入,v1 a2
得t2=10+2a1 10
根据牛顿第二定律得,下滑时有:mgsin37°-μmgcos37°=ma3.
代入数据解得a3=2m/s2.
x3=
a3t32,将a3=2m/s2和t3=3-t2=3-1 2
代入,10+2a1 10
得x3=(3-
)2.10+2a1 10
由几何关系可知,x1+x2-x3=49m.
得20+2a1+
-(3-(10+2a1)2 20
)2=49m.10+2a1 10
化简为:a12+30a1-175=0
解得a1=5m/s2.
所以F=20+2a1=30N.
答:(1)刚撤去推力F时滑块的加速度大小为10m/s2.
(2)推力F的大小为30N.
