问题
问答题
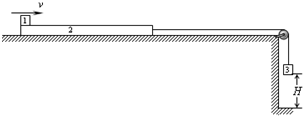
如图所示,有1、2、3三个质量均为m=1kg的物体,物体2与物体3通过不可伸长轻绳连接,跨过光滑的定滑轮,设长板2到定滑轮足够远,物体3离地面高H=5.75m,物体1与长板2之间的动摩擦因数μ=0.2.长板2在光滑的桌面上从静止开始释放,同时物体1(视为质点)在长板2的左端以v=4m/s的初速度开始运动,运动过程中恰好没有从长板2的右端掉下.求:
(1)长板2的长度L0;
(2)当物体3落地时,物体1在长板2的位置.
答案
设向右为正方向(1)物体1的加速度:
a1=-
=-μg=-2m/s2μmg m
物体2和3的整体加速度为:
a2=
=6m/s2.mg+μmg 2m
设经过时间t1二者速度相等 即有:v1=v+a1t=a2t
代入数据t1=0.5m/s,v1=3m/s
物体1的位移为:x1=
t=1.75mv+v1 2
物体1的位移为:x2=
tv1 2
所以木板2的长度L0=x1-x2=1m.
(2)此后,假设物体123相对静止,a=
g,1 3
物体1受到的静摩擦力为 Ff1=ma=3.3N>Ff=μmg=2N,故假设不成立,则知物体1和物体2相对滑动.
物体1的加速度大小为 a3=μg=2m/s2
物体2和3整体的加速度大小为 a4=
=4m/s2mg-μmg 2m
整体下落高度h=H-x2=5m,
根据h=v1t+
a4t22 解得 t2=1s1 2
物体1的位移x3=v1t2+
a3t22=4m1 2
则h-x3=1m
故物体1在长木板2的最左端.
答:
(1)长板2的长度L0是1m.
(2)当物体3落地时,物体1在长板2的最左端.