问题
选择题
由一根内壁光滑的玻璃管构成一个直角三角形处于竖直平面内，倾斜角为θ=37°，让两个相同的小球同时从顶端A静止开始出发．一个球沿AC做加速度大小为a=gsin37°的匀加速运动至C，到达C所用的时间为t1，另一个球竖直自由下落经过B后匀速运动到达C，所用的时间为t2，在转弯处有个极小的光滑圆弧，可确保小球转弯时速度大小不变，且转弯时间可以忽略不计．（其中sin37°=0.6，cos37°=0.8）．比较t1与t2的关系（ ）
A．t1＜t2
B．t1=t2
C．t1＞t2
D．条件不够无法确定
答案
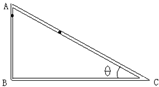
设斜面长为x，右球做匀加速直线运动，根据x=
at22得：t2=1 2
=2x a
=2x gsin30° x 3
球自由落体运动时间t=
=2h g
=2xsin37° g 0.6x 5
最大速度为v=
=2gh
=2gxsin37° 12x
匀速时间为t′=
=0.40.8x v x 3
总时间为：t1=t+t′=
+0.40.6x 5
=x 3 x 3
故t1=t2；
故选：B．
