问题
计算题
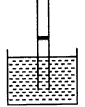
如图所示，一根两端开口、横截面积为S=2 cm2足够长的玻璃管竖直插入水银槽中并固定（插入水银槽中的部分足够深）。管中有一个质量不计的光滑活塞，活塞下封闭着长L=21 cm的气柱，气体的温度t1=7℃，外界大气压取P0=1.0×l05 Pa（相当于75 cm汞柱高的压强）。
（1）对气体加热，使其温度升高到t2=47℃，此时气柱为多长？
（2）在活塞上施加一个竖直向下的压力F=4 N，保持气体的温度t2不变，平衡后活塞下降的高度为多少？（以上过程中水银槽中的液面高度可视为不变）
答案
解：（1）被封闭气体的初状态为P1=P0=l.0×105 Pa=75 cmHg，V1=L1S=21S，T1=280 K
末态为P2=p0=1.0×l05 Pa=75 cmHg，V2=L2S，T2=320K
根据盖·吕萨克定律有
，即
得
（2）在活塞上施加压力F后，气体的状态变为
=1.2×l05 Pa=90 cmHg，V3=L3S，T3=T2=320 K
根据玻意耳定律，有p3V3=p2V2，即p3L3=P2L2
由于△p=p3－v0=90－75 cmHg=15 cmHg
所以管内外水银面的高度差为△h=15 cm
活塞下降的高度h=△h+L2－L3=19 cm