问题
问答题
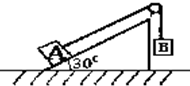
如图所示,可视为质点的两物块A、B,质量分别为m、2m,A放在一倾角为30°并固定在水平面上的光滑斜面上,一不可伸长的柔软轻绳跨过光滑轻质定滑轮,两端分别与A、B相连接.托住B使两物块处于静止状态,此时B距地面高度为h,轻绳刚好拉紧,A和滑轮间的轻绳与斜面平行.现将B从静止释放,斜面足够长.重力加速度为g.求:
(1)B落地前绳中张力的大小F;
(2)整个过程中A沿斜面向上运动的时间t.
答案
(1)设B落地前两物块加速度大小为a,对于A,取沿斜面向上为正,对于B,取竖直向下为正.由牛顿第二定律得:
T-mgsin30°=ma
2mg-T=2ma
解得:a=
g.1 2
T=mg.
(2)设B落地前瞬间A的速度为v,由运动学公式得:
V2=2ah
设B落地后,A沿斜面向上运动的过程中加速度为a1,则:
a1=gsin30°
设B落地后,A沿斜面向上运动的最大距离为S,由运动学公式得:
-V2=2a1S
S=
vt21 2
解得:S=h
t2=t1=
=22h a h g
则整个过程A沿斜面向上运动的最大距离为:
t=t1+t2=4
.h g
答:(1)B落地前绳中张力的大小为mg.
(2)整个过程中A沿斜面向上运动的时间为4
.h g
