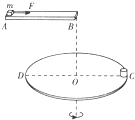
如图所示，水平放置的圆盘半径为R=1m，在其边缘C点固定一个高度不计的小桶，在圆盘直径CD的正上方放置一条水平滑道AB，滑道与CD平行．滑道右端B与圆盘圆心O在同一竖直线上，其高度差为h=1.25m．在滑道左端静止放置质量为m=0.4kg的物块（可视为质点），物体与滑道间的动摩擦因数为μ=0.2．当用一大小为F=4N的水平向右拉力拉动物块的同时，圆盘从图示位置以角速度ω=2πrad/s，绕穿过圆心O的竖直轴匀速转动，拉力作用一段时间后撤掉，物块在滑道上继续滑行，由B点水平抛出，恰好落入小桶内，重力加速度取10m/s2．
（1）物块离开B点水平抛出的初速度vB；
（2）分别求出拉力撤掉前后物块的加速度a1和a2；
（3）若拉力作用时间为0.5s，求所需滑道的长度L；
（4）调整拉力的作用时间和滑道的长度，物块仍恰好落入小桶内，求拉力作用的最短时间．
（1）物块平抛：h=
gt2；1 2
得：t=
=0.5s2h g
物块离开滑道时的速度：v=
=R t
=2m/s1 0.5
（2）拉动物块时的加速度为a1，由牛顿第二定律：F-μmg=ma1
代入数据得：a1=8m/s2
撤去拉力后，由牛顿第二定律得：
-μmg=ma2；
代入数据得：a2=-2m/s2
（3）物块加速的末速度：v1=a1t1′=8×0.5=4m/s
则板长为：L=x1+x2=
a1t1′2+1 2
=v2-v12 2a2
×8×0.25+1 2
=4m．4-16 2×(-2)
（4）盘转过一圈时落入，拉力时间最短；盘转过一圈时间为：
T=
=1s2π ω
物块在滑道上先加速后减速，有：v=a1t1+a2t2
物块滑行时间、抛出在空中时间与圆盘周期关系：t1+t2+t=T
由上两式得：t1=0.3s．
答：（1）物块离开B点水平抛出的初速度为2m/s；
（2）分别求出拉力撤掉前后物块的加速度a1和a2分别为8m/s2、-2m/s2．
（3）所需滑道的长度L为4m；
（4）拉力作用的最短时间为0.3s．