问题
计算题
如图，在大气中有一水平放置的固定圆筒，它由a、b和c三个粗细不同的部分连接而成，各部分的横截而积分别为2S、1/2S和S。已知大气压强为p0，温度为T0。两活塞A和B用一根长为4l的不可伸长的轻线相连，把温度为T0的空气密封在两活塞之间，此时两活塞的位置如图所示现对被密封的气体加热，使其温度缓慢上升到T若活塞与圆筒壁之间的摩擦可忽略，此时两活塞之间气体的压强可能为多少？
答案
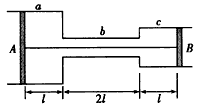
解：设加热前，被密封气体的压强为P1，轻线的张力为f。
因两活塞都处在静止状态，对活塞A有2P0S -2p1S+f=0 ①
对活塞B有p1S-P0S-f=0 ②
由①②式得p1= P0③
f=0 ④
即被密封气体的压强与大气压强相等，轻线处在拉直的松弛状态，
这时气体的体积V1= 2S1+S1+ S1=4S1 ⑤
对气体加热时，被密封气体温度缓慢升高，两活塞一起向左缓慢移动，气体体积增大，压强保持p1不变，若持续加热，此过程会一直持续到活塞向左移动的距离等于l为止，
这时气体的体积V1=4S1+S1=5S1⑥
设此时气体的温度为T2，由盖·吕萨克定律V2∝T2，即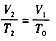
⑦
由③⑤⑥⑦得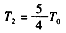
⑧
由此可知，当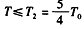
时，气体的压强P2=P0⑨
当T>T2时，活塞已无法移动，被密封气体的体积保持V2不变，
气体经历一等容升压过程当气体的温度为T时，设其压强为p，由查理定律p∝T，即有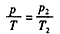
⑩
即当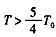
时，气体的压强为
。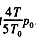