问题
问答题
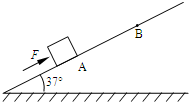
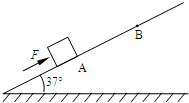
如图,倾角为37°、足够长的斜面体固定在水平地面上,小木块在沿斜面向上的恒定外力F作用下,从斜面上的A点由静止开始向上作匀加速运动,前进了4.0m抵达B点时,速度为8m/s.已知木块与斜面间的动摩擦因数μ=0.5,木块质量m=1kg.g取10m/s2,sin37°=0.6,cos37°=0.8.
(1)小木块从A点运动到B点过程的加速度大小是多少?
(2)木块所受的外力F多大?
(3)为使小木块通过B点的速率为8 5
m/s,求恒力F连续作用的最长时间t.5
答案
(1)由匀加速直线运动的规律得:
v2=2a1s
解得:a1=
=8m/s282 2×4
(2)由牛顿第二定律得:
F-mgsinθ-μmgcosθ=ma1
代入数据可求得:F=18N
(3)当小木块运动一段时间后撤去外力,且向下运动经过B点的速度为8 5
m/s时,恒力作用的时间有最大值.设小木块继续上滑的加速度为a2:5
a2=gsinθ+μgcosθ=10m/s2
设小木块向下运动的加速度为a3,则:
a3=gsinθ-μgcosθ=2m/s2
向下运动至B点的距离为S3,则:
v2=2a3s3
设恒力作用的最长时间为t1,撤去恒力向上减速至零所用时间为t2,则:
a1t1=a2t2
a11 2
+t 21
a21 2
=s1+s3t 22
联立解得:t1=1s
答:(1)小木块从A点运动到B点过程的加速度大小是8m/s2
(2)木块所受的外力F18N
(3)为使小木块通过B点的速率为8 5
m/s,恒力F连续作用的最长时间1s5