问题
解答题
如图，已知射线CB∥OA，∠C=∠OAB=100°，E、F在CB上，且满足∠FOB=∠AOB，OE平分∠COF
（1）求∠EOB的度数.
（2）若平行移动AB，那么∠OBC：∠OFC的值是否随之发生变化？若变化，找出变化规律；若不变，求出这个比值.
（3）在平行移动AB的过程中，是否存在某种情况，使∠OEC=∠OBA？若存在，求出其度数；若不存在，说明理由.
答案
解:（1） 因为CB∥OA，∠C=∠OAB=100°，
所以∠COA=180°－100°=80°，
又因为E、F在CB上，∠FOB=∠AOB，OE平分∠COF，
所以∠EOB=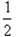
∠COA=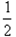
×80°=40°.
（2）不变，
因为CB∥OA，
所以∠CBO=∠BOA，
又∠FOB=∠AOB，
所以∠FOB=∠OBC，而∠FOB+∠OBC=∠OFC，即∠OFC=2∠OBC，
所以∠OBC：∠OFC=1：2.
（3）存在某种情况，使∠OEC=∠OBA，此时∠OEC=∠OBA=60°.
理由如下：
因为 ∠COE+∠CEO+∠C=180°，∠BOA+∠OAB+∠ABO=180°，且∠OEC=∠OBA，∠C=∠OAB=100°，
所以∠COE =∠BOA，
又因为∠FOB=∠AOB，OE平分∠COF，
所以∠BOA=∠BOF=∠FOE=∠EOC=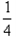
∠COA=20°，
所以∠OEC=∠OBA=60°.