如图所示,甲、乙两小球静止在光滑水平面上,甲、乙的质量分别是2kg和1kg,在强大的内力作用下分离,分离时甲的速度v1=2m/s,乙小球冲上速度为v0=2m/s的水平传送带上(传送带速度保持不变),乙与传送带之间的动摩擦因数μ=0.2,DEF是光滑细圆管,其中D点与水平面相切,EF是半经为R=0.1m圆弧,乙小球的直经比细管直经略小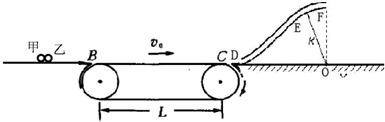 点,乙小球离开传送带时与传送带速度相等,从D处进入细管到达细管的最高点F水平飞出,求:
点,乙小球离开传送带时与传送带速度相等,从D处进入细管到达细管的最高点F水平飞出,求:
(1)乙小球冲上传送带时的速度;
(2)传送带的水平距离L应满足的条件?
(3)乙小球运动到细管的最高点F时对细管的作用力(要回答对细管上壁还是下壁的作用力)
(1)甲、乙两小球组成的系统动量守恒,以甲的速度方向为正方向,由动量守恒定律得:
m甲v甲-m乙v乙=0,
代入数据解得:v乙=4m/s;
(2)v乙>v0,乙小球在传送带上做匀减速运动,对乙,由牛顿第二定律得:
a=
=f m乙
=μg,μm乙g m乙
由匀变速运动的速度位移公式得,乙的位移:s=
=3m,
-v 2乙 v 20 2a
传送带水平距离应满足的条件是:L≥s=3m;
(3)球由D到F过程中,由机械能守恒定律得:
m1 2
=v 20
m1 2
+mgR,v 2
代入数据解得:v=
m/s,2
乙小球在最高点F,由牛顿第二定律得:mg+F=m
,v2 R
代入数据解得:F=10N,
F是正值说明是细管的上壁对小球有向下的压力,
由牛顿第三定律知,小球对细管的上壁有向上的作用力,大小10N;
答:(1)乙小球冲上传送带时的速度为4m/s;
(2)传送带的水平距离L应满足L≥3m;
(3)乙小球运动到细管的最高点F时,小球对细管的上壁有向上的作用力,大小10N.
