问题
计算题
半径分别为r和2r的同心圆形导轨固定在同一水平面上，一长为r，质量为m且质量分布均匀的直导体棒AB置于圆导轨上面，BA的延长线通过圆导轨的中心O，装置的俯视图如图所示；整个装置位于一匀强磁场中，磁感应强度的大小为B，方向竖直向下；在内圆导轨的C点和外圆导轨的D点之间接有一阻值为R的电阻（图中未画出）。直导体棒在水平外力作用下以角速度ω绕O逆时针匀速转动，在转动过程中始终与导轨保持良好接触。设导体棒与导轨之间的动摩擦因数为μ，导体棒和导轨的电阻均可忽略，重力加速度大小为g，
求：（1）通过电阻R的感应电流的方向和大小；
（2）外力的功率。
答案
（1）
（2）
题目分析：（1）在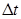
时间内，导体棒扫过的面积为：
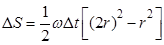①
根据法拉第电磁感应定律，导体棒产生的感应电动势大小为：
②
根据右手定则，感应电流的方向是从B端流向A端，因此流过导体R的电流方向是从C端流向D端；由欧姆定律流过导体R的电流满足;
③
联立①②③可得： ④
（2）在竖直方向有：mg-2N=0 ⑤
式中，由于质量分布均匀，内外圆导轨对导体棒的正压力相等，其值为N，两导轨对运动的导体棒的滑动摩擦力均为：
⑥
在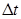时间内，导体棒在内外圆导轨上扫过的弧长分别为：
⑦
和
⑧
克服摩擦力做的总功为：
⑨
在
时间内，消耗在电阻R上的功为：
⑩
根据能量转化和守恒定律，外力在时间内做的功为：
（11）
外力的功率为：
（12）
由④至（12）式可得：（13）