问题
问答题
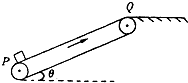
如图所示,绷紧的传送带,始终以2m/s的速度匀速斜向上运行,传送带与水平方向间的夹角θ=30°.现把质量为lOkg的工件轻轻地无初速度放在传送带底端P,由传送带传送至顶端Q,已知PQ之间的距离为4m,工件与传送带间的动摩擦因数为
,取g=10m/s23 2
(1)通过计算说明工件在传送带上做什么运动?
(2)求工件从P点运动到Q点所用的时间.
答案
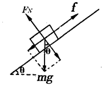
(1)工件刚放上传送带,受力如图:
垂直传送带由平衡得:
N=mgcosθ ①
沿传送带由牛顿第二定律得:f-mgsin=ma. ②
f=μN③
由①②③得:a=2.5 m/s2.
设工件达到2m/s位移为s,则s═0.8(m)<4 m
然后工件做匀速运动到Q端,工件先做匀加速运动再做匀速运动.
(2)工件匀加速运动的时间为:t1═0.8(s)
工件匀速运动的时间为t2═1.6(s)
工件从P点运动到Q点所用时间为:T=t1+t2=2.4(s)
答:(1)工件先做匀加速运动再做匀速运动.
(2)工件从P点运动到Q点所用的时间2.4s.