问题
计算题
如图,粗糙斜面与光滑水平面通过光滑小圆弧平滑连接,斜面倾角θ=37°。A、B是两个质量均为m=1kg的小滑块(可看作质点),B的左端连接一轻质弹簧。若滑块A在斜面上受到F=4N,方向垂直斜面向下的恒力作用时,恰能沿斜面匀速下滑。现撤去F,让滑块A从斜面上,距斜面底端L=1m处,由静止开始下滑。取g=10m/s2,sin37°=0.6,cos37°=0.8。
(1)求滑块A与斜面间的动摩擦因数;
(2)求滑块A到达斜面底端时的速度大小;
(3)滑块A与弹簧接触后粘连在一起。求此后弹簧的最大弹性势能。

答案
解:(1)滑块沿斜面匀速下滑时受力如图1所示
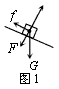
根据牛顿第二定律mgsinθ=μN,N=mgcosθ+F
解得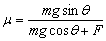 =0.5
=0.5
(2)滑块沿斜面加速下滑时受力如图2所示
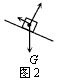
设滑块滑到斜面低端时的速度为v1,根据动能定理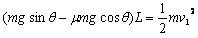
代入数据解得v1=2 m/ s
(3)以A、B、弹簧为研究对象,设它们共同的速度为v2
根据动量守恒定律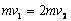
设弹簧的最大弹性势能为Ep,根据能量守恒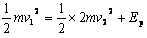
代入数据解得Ep=1J
