问题
问答题
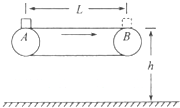
如图所示为某企业流水线上使用的水平传送带装置示意图.绷紧的传送带始终保持恒定速率运行,传送带的水平部分AB距水平地面的高度为h=0.45m.现有一集装箱(可视为质点)由A端被传送到B端,到B端前已与传送带保持相对静止,因没有及时取下,集装箱从B端水平抛出,集装箱与传送带间的动摩擦因数μ0.20.
(g=l0m/s2,不计空气阻力)
(1)若集装箱的落地点与B端的水平距离为0.60m,求传送带的速率v;
(2)若AB间的距离足够长,集装箱以v0=2.40m/s的速度从A端向右滑上传送带,当集装箱滑上传送带t0=1.00s后,电动机出现故障突然停止转动.求集装箱在传送带上留下的划痕多长?
答案
(1)由平抛运动规律,在竖直方向上有:h=
gt2,1 2
在水平方向上有:x=vt
联立解得v=2.0m/s.
(2)根据牛顿第二定律得,μmg=ma,
解得加速度大小a=μg=2m/s2
集装箱减速的时间t=
=v0-v a
s=0.2s<t0,2.4-2 2
即0.20s-1.00s内,集装箱与传送带保持相对静止.
减速过程中集装箱的位移x1=
t=v0+v 2
×0.2m=0.44m,2.4+2 2
传送带的位移x2=vt=2×0.2m=0.4m
相对位移△x1=x1-x2=0.04m,
电动机停止转动后,集装箱滑行的距离为△x2=
=v2 2a
m=1m,4 4
所以,集装箱留下的痕迹长为△x=△x1+△x2=1.04m.
答:(1)传送带的速率为2m/s;
(2)集装箱在传送带上留下的划痕长度为1.04m.
