问题
问答题
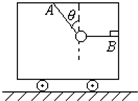
小车在水平面上向左作直线运动,车厢内用OA、OB两细线系住小球.球的质量m=4千克.线OA与竖直方向成θ=37°角.如图所示.g取10米/秒2,
求:(1)小车以5米/秒的速度作匀速直线运动,求OA、OB两绳的张力?
(2)小车以5米/秒的速度作匀速直线运动,当小车改作匀减速直线运动,并在12.5米距离内速度降为零的过程中,OA、OB两绳张力各多大?
(3)小车如何运动时,可使OB绳所受拉力开始为零?
答案
依题意(1)选小球为研究对象,
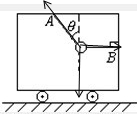
X轴方向水平向左,根据平衡条件:
X轴:TAOsinθ-TBO=0
Y轴:TAOcosθ-mg=0
解得:TAO=50N TBO=30N;
(2)设小车运动方向为正方向,作匀减速的初速度v0=5m/s,末速度为0,s=12.5m
由
=2asv 2t
得小车做匀减速的加速度为:a=-1m/s2
X轴:TAOsinθ-TBO=ma
Y轴:TAOcosθ-mg=0
解得:TAO=50N;TBO=34N;
(3)当绳子OB所受拉力恰好为零时,则
X轴:TAOsinθ=ma
Y轴:TAOcosθ-mg=0
解得a=7.5m/s2
即小车向左做加速度大于a=7.5m/s2的运动;
答:(1)小车以5米/秒的速度作匀速直线运动,OA、OB两绳的张力分别为50N、30N.
(2)小车以5米/秒的速度作匀速直线运动,当小车改作匀减速直线运动,并在12.5米距离内速度降为零的过程中,OA、OB两绳张力分别为50N、34N.
(3)小车向左做加速度大于a=7.5m/s2的运动,可使OB绳所受拉力开始为零.
