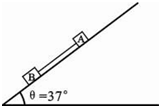
如图所示,斜面与水平面间的夹角θ=37°,物体A和B的质量分别为mA=10kg、mB=5kg.A、B间用质量不计的细绳相连.试求:
(1)当斜面光滑时,两个物体的加速度及绳的张力各是多少?
(2)当A和B与斜面间的动摩擦因数为μ=0.2时,两个物体的加速度及绳的张力各是多少?
(3)当A和B与斜面间的动摩擦因数分别为μA=0.2、μB=0.8时,则释放后的开始阶段,两个物体的加速度及绳的张力又各是多少?
(1)如斜面光滑摩擦不计,
用整体法:(mA+mB)gsinθ=(mA+mB)a,
解得:a=gsinθ=6m/s2
用隔离法对B:mBgsinθ-FT=mBa,代入数据求出FT=0
(2)用整体法:(mA+mB)gsinθ-μ(mA+mB)gcosθ=(mA+mB)a,
解得:a=gsinθ-μAgcosθ=4.4m/s2
用隔离法对B:mBgsinθ-μBmBgcosθ-FT=mBa,
代入数据求出FT=0
(3)用隔离法对B:因为mBgsinθ<μBmBgcosθ
所以物体B不下滑,物体A下滑,绳松弛,FT=0.
所以aA=g(sinθ-μAcosθ)=4.4m/s2
答:(1)当斜面光滑时,两个物体的加速度为6m/s2,绳的张力都为零.
(2)当A和B与斜面间的动摩擦因数为μ=0.2时,两个物体的加速度为4.4m/s2,绳的张力为零;
(3)当A和B与斜面间的动摩擦因数分别为μA=0.2、μB=0.8时,释放后的开始阶段,A的加速度为4.4m/s2,B的加速度为零,绳的张力为零.
