问题
问答题
如图所示,ABC为一细圆管构成的
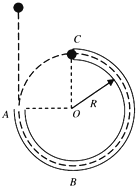
圆轨道,将其固定在竖直平面内,轨道半径为R(比细圆管的半径大得多),OA水平,OC竖直,最低点为B,最高点为C,细圆管内壁光滑.在A点正上方某位置有一质量为m的小球(可视为质点)由静止开始下落,刚好进入细圆管内运动.已知细圆管的内径稍大于小球的直径,不计空气阻力.3 4
(1)若小球经过C点时恰与管壁没有相互作用,求小球经过C点时的速度大小;
(2)若小球刚好能到达轨道的最高点C,求小球经过最低点B时的速度大小和轨道对小球的作用力大小;
(3)若小球从C点水平飞出后恰好能落回到A点,求小球刚开始下落时距离A点的高度.
答案
(1)设通过C点时小球速度为vc,
小球与管壁没有相互作用,则重力充当向心力,即:mg=m v 2c R
解得:vc=gR
(2)小球恰好通过C点,故小球通过C点的速度为零,
对小球由B到C的过程根据动能定理,有:0-
m1 2
=mg2R ①v 2B
又由小球经过B点时,由牛顿第二定律:FN-mg=
②m v 2B R
①②联立可得:vB=2
,FN=5mgRg
(3)小球从C点飞出后做平抛运动,
竖直方向:R=
gt21 2
水平方向:R=vc′t
解得:vc′=gR 2
由初末机械能守恒可得:mg(h-R)=
m1 2 v′ 2c
解得:h=
R5 4
答:(1)若小球经过C点时恰与管壁没有相互作用,小球经过C点时的速度大小为
;gR
(2)若小球刚好能到达轨道的最高点C,小球经过最低点B时的速度大小为2
,轨道对小球的作用力大小为5mg;Rg
(3)若小球从C点水平飞出后恰好能落回到A点,小球刚开始下落时距离A点的高度为
R.5 4
