问题
问答题
已知函数f(x)和g(x)的图象关于原点对称,且f(x)=x2+2x,
(Ⅰ)求函数g(x)的解析式;
(Ⅱ)解不等式g(x)≥f(x)-|x-1|;
(Ⅲ)若h(x)=g(x)-λf(x)+1在[-1,1]上是增函数,求实数λ的取值范围。
答案
参考答案:
(Ⅰ)设函数y=f(x)的图象上任意一点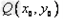 关于原点的对称点为P(x,y),
关于原点的对称点为P(x,y),
则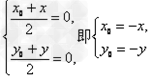 ,
,
∵点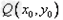 在函数y=f(x)的图象上,
在函数y=f(x)的图象上,
∴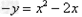 ,即
,即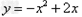 ,故
,故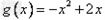 。
。
(Ⅱ)由 ,可得
,可得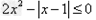 ,
,
当x≥1时,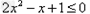 ,此时不等式无解;
,此时不等式无解;
当x<1时,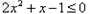 ,解得
,解得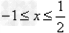 ;
;
因此,原不等式的解集为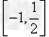 。
。
(Ⅲ)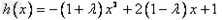 ,
,
①当λ=-1时,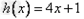 在[-1,1]上是增函数, ∴λ=-1;
在[-1,1]上是增函数, ∴λ=-1;
②当λ≠-1时,对称轴的方程为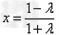 ,
,
ⅰ)当λ<-1时,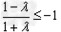 ,解得λ<-1;
,解得λ<-1;
ⅱ)当λ>-1时, ,解得-1<λ≤0;
,解得-1<λ≤0;
综上,λ≤0。
