问题
计算题
如图所示,凹槽的水平底面宽度s=0.3m,左侧高度H=0.45m,右侧高度h=0.25m。凹槽的左侧竖直面与半径R=0.2m的1/4光滑圆弧轨道相接,A和B分别是圆弧的端点,右侧竖直面与水平面MN相接。小球P1静止从A点沿圆弧轨道滑下,与静置于B点的小球P2发生弹性碰撞。P2的质量m=1kg,P1的质量是P2质量的k倍。已知重力加速度g=10m/s2,不计空气阻力。
(1)求小球P1从圆弧轨道滑至B点时的速度大小;
(2)若小球P2碰撞后第一落点在M点,求碰撞后P2的速度大小;
(3)设小球P2的第一落点与凹槽左侧竖直面的水平距离为x,试求x的表达式。

答案
解:(1)P1从A点滑至B点过程中,根据动能定理有: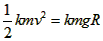
解得在B点的速度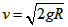 =2m/s
=2m/s
(2)小球P2从B点到M点,根据平抛运动规律有: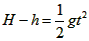
得下落时间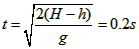
由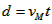 解得小球P1从C点抛出时的速度
解得小球P1从C点抛出时的速度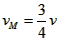 =1.5m/s
=1.5m/s
(3)根据动量守恒定律有: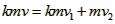
根据能量守恒有: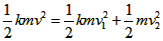
解得: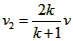
①若P2落在MN水平面,则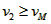
解得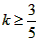
即当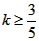 时,
时,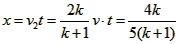
②当P2落在凹槽底面时,落地时间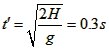
最大抛出速度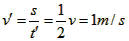
所以若P2落在凹槽底面时,则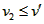 ,解得
,解得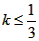
即当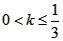 时,
时,
③当 时,P2落在右侧竖直面上,故
时,P2落在右侧竖直面上,故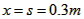 。
。
