问题
计算题
（10分）一架军用直升机悬停在距离地面64 m的高处，将一箱军用物资由静止开始投下，如果不打开物资上的自动减速伞，物资经4s落地。为了防止物资与地面的剧烈撞击，须在物资距离地面一定高度时将物资上携带的自动减速伞打开。已知物资接触地面的安全限速为2m/s，减速伞打开后物资所受空气阻力是打开前的18倍。减速伞打开前后空气阻力均认为大小不变，忽略减速伞打开的时间，取g="10" m/s2。求：
（1）减速伞打开后物资的加速度为多大？
（2）减速伞打开时物资速度最多为多少？
答案
（1）
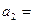26m/s2
（2）v0=28m/s
设物资质量为m，不打开伞的情况下，
物资经t=4s落地。由牛顿第二定律和运动学公式得
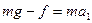（1分）
（1分）
解得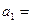 
8m/s2，
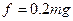（2分）
设物资落地速度恰为v=2m/s时，减速伞打开的高度为h，开伞时物资的速度为v0，由牛顿第二定
律和运动学公式得
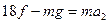（2分）
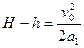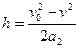（1分） 
（1分）
解得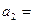：26m/s2 （1分） v0="28m/s " （1分）