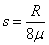问题
计算题
如图所示,一条轨道固定在竖直平面内,粗糙的ab段水平,bcde段光滑,cde段是以O为圆心、R为半径的一小段圆弧。可视为质点的物块A和B紧靠在一起,静止于b处,A的质量是B的3倍。两物块在足够大的内力作用下突然分离,分别向左、右始终沿轨道运动。B到d点时速度沿水平方向,此时轨道对B的支持力大小等于B所受重力的3/4,A与ab段的动摩擦因数为μ,重力加速度g,求:
(1)物块B在d点的速度大小;
(2)物块A滑行的距离s。

答案
解:(1)B在d点,根据牛顿第二定律有: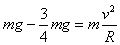
解得: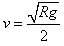
(2)B从b到d过程,只有重力做功,机械能守恒有: ①
①
AB分离过程动量守恒有: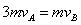 ②
②
A匀减速直线运动,用动能定理得: ③
③
联立①②③,解得: