问题
问答题
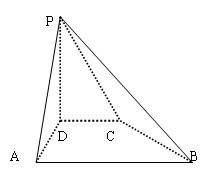
如图,四棱锥P—ABCD中,PD⊥平面ABCD,PA与平面ABCD所成的角为60°,在四边形ABCD中,∠CDA=∠DAB=90°,AB=4,CD=1,AD=2.(1)建立适当的坐标系,并写出B、P的坐标;(2)求异面直线PA与BC所成的角;(3)若PB的中点为M,求证:平面AMC⊥平面PBC.
答案
参考答案:
(1)解:建立如上图所示的直角坐标系D—xyz,
∵∠D=∠DAB=90°,AB=4,CD=1,AD=2, ∴
A(2,0,0),C(0,1,0),B(2,4,0).
由PD⊥平面ABCD,得∠PAD为PA与平面ABCD所成的角.∴∠PAD=60°.
在Rt△PAD中,由AD=2,得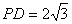 .
.
∴P(0,0, ).
).
(2)解:∵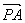 =(2,0,
=(2,0,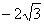 ),
),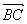 =(-2,-3,0),
=(-2,-3,0),
∴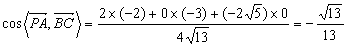 .
.
∴PA与BC所成的角为arccos .
.
(3)证明:∵M为PB的中点, ∴点M的坐标为(1,2,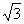 ).
).
∴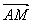 =(-1,2,
=(-1,2,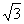 ),=(1,1,
),=(1,1,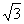 ),=(2,4,
),=(2,4,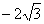 ).
).
∵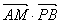 =(-1)×2+2×4+
=(-1)×2+2×4+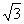 ×(
×(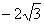 )=0,
)=0,
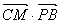 =1×2+1×4+
=1×2+1×4+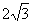 ×(
×(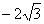 )=0,
)=0,
∴ ,
,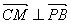 .
.
∴PB⊥平面AMC. 又PB面PCB, ∴平面AMC⊥平面PBC.
启示:异面直线所成角的范围为(0,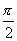 ).
).
