（16分）在光滑水平面上有一质量m=1.0×10-3kg的小球，静止在O点，以O点为原点，在该水平面内建立直角坐标系Oxy，如图所示.现突然加一沿x轴正方向、大小为F=2.0×10-4N的恒力，使小球开始运动，经过1.0s，所加恒力突然变为沿y轴正方向，大小仍为F=2.0×10-4N的恒力，再经过1.0s所加恒力又突然变为另一个恒力.使小球在此恒力作用下经1.0s速度变为0.求此恒力及速度为0时小球的位置.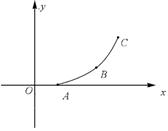
F=0.2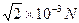
，小球到达的位置坐标为
x3=0.40m，y3=0.20m
由牛顿定律可知小球的加速度
a=F/m=0.20m/s2. ----------------------------------------------------------------------------------------------（1分）
当F沿x轴正方向时，经1.0s小球
的速度大小为vx="at=0.20×1.0=0.20m/s" ------------------------------------------（1分）
（方向沿x轴方向）
小球沿x轴方向移动的距离为△x1=at2/2=0.10m.---------------------------------（1分）
在第2s内，F方向y轴正方向，x方向不再受力，
所以第2s内小球在x方向做匀速运动，在y方向做初速度为0的匀加速直线运动（类似平抛运动）-------------（1分）沿y方向的距离:△y=at2/2=0.10m.-------（1分）
沿x方向的距离:△x2=vxt=0.2×1.0=0.20m.--------------（1分）
第2s未在y方向分速度为:
vy=at=0.20×1.0=0.20m/s-------------------（1分）
由上可知，此时小球运动方向与x轴成45°角，要使小球速度变为0，则在第3s内所加恒力方向必须与此方向相反，即指向第三象限，与x轴成225°角.--------------（2分）
在第3s内，设在电场作用下小球加速度的x分量和y方向分量分别为ax、ay，则
ax=vx/t=0.2m/s2，---------------（0.5分）
ay=vy/t=0.20m/s2；-----------------------（0.5分）
此恒力的大小F=ma=0.2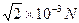-------------（2分）
在第3s未，小球到达的位置坐标为
x3=△x1+△x2+vxt-axt2/2=0.40m，----------------（2分）
y3=△y+vyt-ayt2/2="0.20m " --------------------- (2分)
