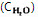问题
解答题
在△ABC中,C-A=
(1)求sinA的值; (2)设AC=
|
答案
(1)由C-A=
和A+B+C=π,π 2
得2A=
-B,0<A<π 2
.π 4
故cos2A=sinB,即1-2sin2A=
,sinA=1 3
.3 3
(2)由(1)得cosA=
.6 3
又由正弦定理,得
=BC sinA
,BC=AC sinB
•AC=sinA sinB
×3 3 1 3
=36
.2
∵C-A=
,∴C=π 2
+A,π 2
sinC=sin(
+A)=cosA,π 2
∴S△ABC=
AC•BC•sinC=1 2
AC•BC•cosA1 2
=
×1 2
×36
×2
=36 3
.2