问题
计算题
如图水平传送带沿顺时针匀速转动,在传送带上的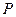 点轻放一质量
点轻放一质量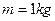 的小物块。小物块随传送带运动到
的小物块。小物块随传送带运动到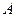 点后水平抛出,恰好沿圆弧切线从
点后水平抛出,恰好沿圆弧切线从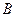 点进入竖直光滑圆孤轨道运动。如图
点进入竖直光滑圆孤轨道运动。如图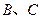 为圆弧的两端点。小物块离开
为圆弧的两端点。小物块离开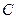 点后沿固定斜面向上运动,经
点后沿固定斜面向上运动,经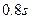 第二次通过
第二次通过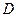 点。己知小物块与传送带问的动摩擦因数
点。己知小物块与传送带问的动摩擦因数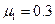 ,圆弧半径
,圆弧半径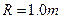 ,圆弧对应的圆心角
,圆弧对应的圆心角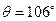 ,
,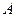 点距地面的高度
点距地面的高度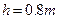 ,小物块与斜面间的动摩擦因数
,小物块与斜面间的动摩擦因数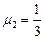 ,(重力加速度
,(重力加速度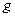 取
取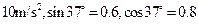 )试求:
)试求:
(1)小物块到达B点的速度VB和离开A点的速度VA;
(2)若传送带的速度为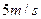 ,则
,则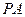 间的距离是多大?
间的距离是多大?
(3)斜面上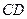 间的距离。
间的距离。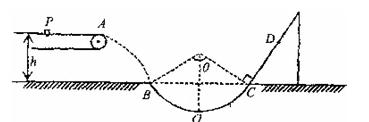
答案
(1) (2)
(2)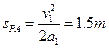 (3)
(3)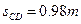
(1)对小物块,由 到
到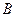 在竖直方向有
在竖直方向有 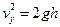 在
在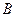 点
点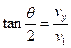
代入数据解得 
(2)小物块在传送带上加速过程: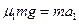 ,
,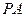 间的距离
间的距离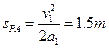
(3)小物块沿斜面上滑,由牛顿第二定律得 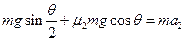
代入数据解得 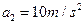 ,
,
小物块沿斜面下滑,由牛顿第二定律得 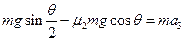
代入数据解得 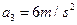
由机械能守恒定律知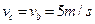 ,小物块由
,小物块由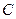 上升到最高点历时
上升到最高点历时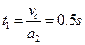
小物块由最高点回到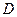 点历时
点历时 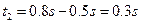 ,故
,故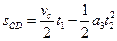
代入数据解得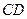 间的距离
间的距离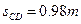 (其他求解方法,均可得分)
(其他求解方法,均可得分)
