问题
单项选择题
当x≠0时设
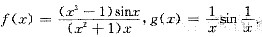 下述命题
下述命题
①对任意x>0,在0<|x|<X上f(x)有界,但在(-∞,+∞)(x≠0)上f(x)无界.
②在(-∞,+∞)(x≠0)上f(x)有界.
③g(x)在x=0的去心邻域内无界,但
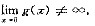
④
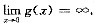
正确的是
答案
参考答案:C
解析:因为[*],所以存在δ>0,在0<|x|<δ上f(x)有界.又[*]1,所以存在X>0,在|x|>X上[*]有界.而函数sinx是有界的,所以在|x|>x上f(x)有界.而在区间[-X,-δ,[δ,X]上f(x)是连续的,所以是有界的,于是知在(-∞,+∞)上f(x)是有界的.②正确.
以下证明③也是正确的.对于任给的M>0,取[*],有
[*]
当[*]时,f(xn)>M.即对于任给的M>0,总存在xn,其中[*](这种n总是有的),使g(xn)>M,说明g(x)在x=0的去心邻域内无界.但另一方面,若取[*]则有g(x’n)=0.此说明
[*]
所以③正确.选(C).
[评注] 将来到第二章还会见到用导数讨论函数的有界(无界)问题.
