问题
问答题
设f(x)=x-(ax+bsinx)cosx，并设
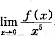存在且不为零，求常数a、b及此极限值．
答案
参考答案：[解] 方法1 所给极限为[*]并且f(x)及x5在x=0的某邻域可求任意阶导数．用洛必达法则，当下式右边极限存在或为∞时，下式左边应与右边相等：
[*]
当x→0时，上式右边分子趋于1-(a+b)．若1-(a+b)≠0，则上式趋于∞，从而与题设[*]存在相矛盾．故
1-(a+b)=0．
于是所求极限的右边为[*]再用洛必达法则，当下式右边极限存在或为∞时，下式左边与右边相等：
[*]
上式右边为[*]再用洛必达法则，当下式右边极限存在或为∞时，下式左边应与右边相等．
[*]
与上述推导的理由类似推知
3a+4b=0．
将它与1-(a+b)=0联立，解得a=4，b=-3．再用洛必达法则，得到
[*]
以a=4，b=-3，代入上式，得原极限为[*]
方法2 上述方法1用洛必达法则推导，运算麻烦，可否用洛必达法则要讨论(要步步讨论)．若用佩亚诺余项泰勒公式展开分子至o(x5)，将是十分方便．由
[*]
有
[*]
由题设
[*]
存在且不为零，所以
[*]
解得a=4，b=-3，从而
[*]
解析：[评注] 在可以用佩亚诺余项泰勒公式情况下，用它比用洛必达法则要快不少．