火车车厢之间由车钩连接,火车起动前车钩间都有间隙。不妨将火车的起动简化成如图所示的情景:在光滑水平面上有19个静止的质量均为m的木箱,自右向左编号依次为0、1、2、3、……18,相邻木箱之间由完全非弹性的钩子连接,当钩子前后两部分相碰时,与钩子相连的两木箱速度立即变为相等。所有木箱均静止时,每一个车钩前后两部分间的距离都为L。
(1)若只给第0号木箱一个水平向右的初速度υ0,求第18号木箱刚运动时速度的大小;
(2)若从某时刻开始,持续对第0号木箱施加向右的水平恒力F,使木箱从静止开始运动,求
(i)第1号木箱刚运动时速度的大小;
(ii)从施加恒力F到第18号木箱开始运动经历的时间。

解:(1)19个木箱相互作用过程满足动量守恒定律,即mυ0=19mυ18
得第18号木箱刚运动时速度的大小υ18=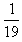 υ0
υ0
(2)(i)若给第0号木箱施加恒定的水平拉力F,第0、1号木箱相互作用前,第0号木箱做匀加速直线运动,加速度大小为a0=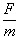
因为υ0′2=2a0L
得第0、1号木箱相互作用前瞬间第0号木箱的速度υ0′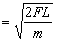
第0、1号木箱相互作用过程满足动量守恒定律,即mυ0′=2mυ1
解得第1号木箱刚运动时速度的大小υ1=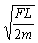
(ii)第1号木箱刚运动时速度的大小(2υ1)2=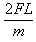 ①
①
第1号木箱与第2号木箱作用前的速度υ1′,有υ1′2-υ12=2a1L
又第1号木箱的加速度大小a1=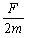
第1、2号木箱相互作用过程满足动量守恒定律,2mυ1′=3mυ2
得第2号木箱刚运动时速度的大小υ2满足(3υ2)2=(2υ1)2+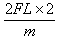 ②
②
同理得第3号木箱刚运动时速度的大小υ3满足(4υ3)2=(3υ2)2+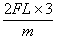 ③
③
……
第18号木箱刚运动时速度的大小υ18满足(19υ18)2=(18υ17)2+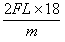 ④
④
累加可得第18号木箱刚运动时速度的大小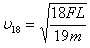
对所有木箱,根据动量定理得Ft=19mυ18
得所求时间