问题
计算题
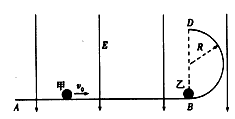
如图，ABD为竖直平面内的光滑绝缘轨道，其中AB段是水平的，BD段为半径R=0.2m的半圆，两段轨道相切于B点，整个轨道处在竖直向下的匀强电场中，场强大小E=5.0×103V/m 一不带电的绝缘小球甲，以速度v0沿水平轨道向右运动，与静止在B点带正电的小球乙发生弹性碰撞，已知甲、乙两球的质量均为m=1.0×10-2kg，乙所带电荷量q=2.0×10-5C，g取10m/a2。（水平轨道足够长，甲、乙两球可视为质点，整个运动过程无电荷转移）
（1）甲、乙两球碰撞后，乙恰能通过轨道的最高点D，求乙在轨道上的首次落点到B点的距离；
（2）在满足（1）的条件下，求甲的速度v0；
（3）若甲仍以速度v0向右运动，增大甲的质量，保持乙的质量不变，求乙在轨道上的首次落点到B点的距离范围。
答案
解：（1）在乙恰能通过轨道最高点的情况下，设乙到达最高点的速度为vD，
乙离开D点到达水平轨道的时间为t，乙的落点到B点的距离为x，则
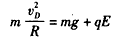①
②
x=vDt ③
联立①②③得x=0.4m ④
（2）设碰撞后甲、乙的速度分别为v甲、v乙
根据动量守恒定律和机械能守恒定律有mv0=mv甲+mv乙 ⑤
联立⑤⑥得v乙=v0⑦
由动能定理，得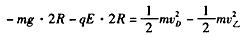
⑧
联立①⑦⑧得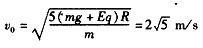
⑨
（3）设甲的质量为M，碰撞后甲、乙的速度分别为vM、vm，
根据动量守恒定律和机械能守恒定律有Mv0= MvM+ mvm⑩
联立⑩得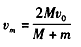
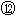
由和M≥m，可得v0≤vm< 2v0 
设乙球过D点时的速度为vDˊ，由动能定理得
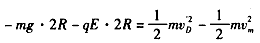
联立⑨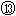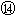得2m/s≤vD'<8m/s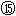 
设乙在水平轨道上的落点距B点的距离为xˊ，有xˊ=vD't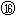 
联立②得0.4m≤xˊ<1.6m。