问题
问答题
设函数f(x)在(-l，l)上连续，在点x=0处可导，且f’(0)≠0．
(Ⅰ) 求证：
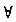给定的0＜x＜1，
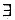0＜θ＜1，使得
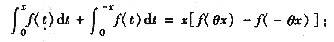
(Ⅱ) 求极限
．
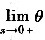答案
参考答案：(Ⅰ) 方法1° 记[*]在(-l，l)内可导．注意F(0)=0，F’(x)=f(x)-f(-x)，由拉格朗日中值定理[*]x∈(0，2)，[*]θ(0＜θ＜1)使
F(x)=F(x)-F(0)=F’(θx)·x=x[f(θx)-f(-θx)]．
方法2° 利用积分中值定理证明．
[*]
其中ξ在0与x之间，故ξ=θx，0＜θ＜1．
(Ⅱ) 为利用f’(0)[*]且≠0，给出θ的表达式．将上式改写成
[*]
注意 [*]
因此，[*]