问题
选择题
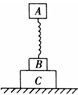
如图所示,木块A与B用一轻弹簧相连,竖直放在木块C上,三者静置于地面上,它们的质量之比是1∶2∶3.设所有接触面都光滑,在沿水平方向抽出木块C的瞬间,木块A和B的加速度分别是( ).
A.aA=0
B.aA=g
C.aB=3g
D.aB=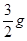
答案
AD
分析:抽出木块C之前,对木块A和木块B分别受力分析,运用平衡条件求出各个力;抽出木块C后,再次对木块A和木块B受力分析,然后根据牛顿第二定律列式求解.
解答:解:抽出木块C之前,木块A受到重力和支持力,有F=mg ①
木块B受到重力2mg、弹簧向下的弹力F和木块C的支持力N,根据平衡条件,有:N=F+mg ②
解得
N=3mg
撤去木块C瞬间,木块C对B的支持力变为零,木块A受力情况不变,故木块A的加速度为零,木块B受重力2mg和弹簧的压力N=mg,故合力为3mg,故物体B的瞬时加速度为1.5mg;
故选A、D.
点评:本题是力学中的瞬时问题,关键是对物体A、B分别受力分析,撤去C物体瞬间再次对物体受力分析,最后运用牛顿第二定律列式求解加速度.
