参考答案：对于实对称矩阵A，若λ是矩阵A的k重特征值，则矩阵A属于特征值λ的特征向量有且只有k个是线性无关的．因此α₁，α₂，α₃必线性相关，那么

故a=1．
(Ⅱ)由秩r(A)=2，知|A|=0，又

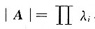，所以A的另一个特征值是λ₃=0．由题设α₁=(1，1，0)^T，α₂=(2，1，1)^T为A的属于特征值6的线性无关的特征向量．设A属于特征值0的特征向量为α=(x₁，x₂，x₃)^T，于是α^T₁α=0，α^T₂α=0即

解得此方程组的基础解系为α=(-1，1，1)^T．那么矩阵A属于特征值λ₃=0的全部特征向量为kα=k(-1，1，1)^T(k为任意非零常数)．
(Ⅲ)设x₁α₁+x₂α₂+x₃α=β，对(α₁，α₂，α|β)作初等行变换，有

解出x₁=3，x₂=-2，x₃=1．
故
β=3α₁-2α₂+α
因为
Aα₁=6α₁，Aα₂=6α₂，Aα=0α
所以
Aⁿβ=3Aⁿα₁-2Aⁿα₂+Aⁿα=3·6ⁿα₁-2·6ⁿα₂=(-6ⁿ，6ⁿ，-2·6ⁿ)^T．
[评注] 本题考查实对称矩阵特征值、特征向量的性质．如果λ是矩阵A的k重特征值，那么λ至多有k个线性无关的特征向量，而作为实对称矩阵，则k重特征值必有k个线性无关的特征向量，从而保证本题中α₁，α₂，α₃一定线性相关，可求出a；要掌握实对称矩阵特征值不同特征向量相互正交这一性质．
本题亦可由A(α¹，α₂，α₃)=(6α₁，6α₂，0α)，先求出矩阵A．然后利用A～A=

而求出Aⁿ=PAⁿP^-1．其中P=(α₁，α₂，α)再来计算Aⁿβ．