问题
问答题
设二维随机变量(X,Y)的概率密度为
f(x,y)=Ae-x2+xy-y2,-∞<x<+∞,-∞<y<+∞
求:(Ⅰ)常数A;
(Ⅱ)fx(z);
(Ⅲ)fY|X(y|x);
(Ⅳ)cov(X,Y).
答案
参考答案:
[分析]: 我们可以从公式
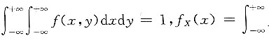 f(x,y)dy和
f(x,y)dy和
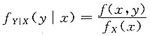 ,fx(x)>0来求出A,fx(x)和fY|X(y|x).而其中A可以从
,fx(x)>0来求出A,fx(x)和fY|X(y|x).而其中A可以从
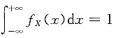 来求出而不必先球
来求出而不必先球
 求cov(X,Y)可用公式cov(X,Y)=EXY-EX·EY.也可以用
求cov(X,Y)可用公式cov(X,Y)=EXY-EX·EY.也可以用
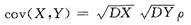 =σ1σ2ρ,其中(X,Y)~N(μ1,μ2;σ21,σ22;ρ).从这点看,还不如将(X,Y)直接理解成一个二维正态随机变量.先求出它的参数,μ1,μ2,σ21,σ22和P.再A,fx(x)从而fY|X(y|x),cov(X,Y)都容易得到.
=σ1σ2ρ,其中(X,Y)~N(μ1,μ2;σ21,σ22;ρ).从这点看,还不如将(X,Y)直接理解成一个二维正态随机变量.先求出它的参数,μ1,μ2,σ21,σ22和P.再A,fx(x)从而fY|X(y|x),cov(X,Y)都容易得到.
[解] 二维正态概率密度一般形式为

而题给条件为f(x,y)=Ae-x2+xy-y2,由此可得
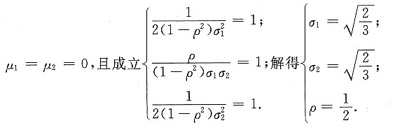
因此
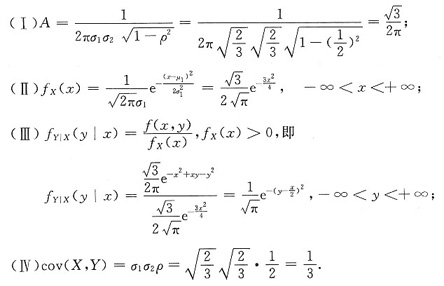

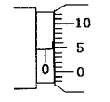
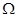 合金丝电阻率的实验, ①用螺旋测微器测定合金丝直径的结果如图所示,合金丝的直径为________mm。
合金丝电阻率的实验, ①用螺旋测微器测定合金丝直径的结果如图所示,合金丝的直径为________mm。