问题
计算题
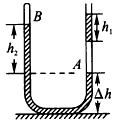
在竖直放置的U形管内由密度为ρ的两部分液体封闭着两段空气柱,大气压强为P0,各部分长度如图所示,求A、B气体的压强。
答案
解法一:平衡法,选与气体接触的液柱为研究对象,进行受力分析,利用平衡条件求解
求pA:取液柱h1为研究对象,设管的横截面积为S,大气压力和液柱重力方向向下,A气体产生的压力方向向上,液柱h1静止,则P0S+ρgh1S=pAS,pA=P0+ρgh1
求pB:取液柱h2为研究对象,由于h2的下端以下液体的对称性,下端液体自重产生的压强可不予考虑,A气体压强由液体传递后对h2的压力方向向上,B气体对h2的压力、液柱h2重力方向向下,液柱平衡,则pBS+ρgh2S=pAS,得pB=P0+ρg(h1-h2)
解法二:取等压面法,根据同种液体在同一液面处的压强相等,在连通器内灵活选取等压面,再由两侧压强相等列方程求解压强
求pB时从A气体下端选取等压面,则有pB+ρgh2=pA=P0+ρgh1
所以pA=P0+ρgh1,pB=P0+ρg(h1-h2)
