问题
填空题
设y=f(x)二阶可导，f’(x)≠0，它的反函数是x=φ(y)，又f(0)=1，f’(0)=
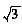，f"(0)=-1，则
=______．
答案
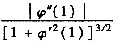参考答案：
[*]
解析：[分析一] 由反函数求导公式得
[*]
再由复合函数求导法得
[*]
从而 [*]
于是 [*]
[分析二] 将上述导出的φ’(y)，φ"(y)表达式代入得
[*]
于是 [*]
[分析三] 在xOy直角坐标系中y=f(x)与它的反函数x=φ(y)代表同一条曲线，作为x的函数y=f(x)与作为y的函数z=φ(y)在同一点处的曲率是相同的，按曲率公式应有
[*]
因f(0)=1，即x=0时y=1[*]
[*]
[*]
类繁多，而数量最大的是青铜礼器。青铜礼器大多烽是王室与贵族祭祀时使用的器皿。夏、商、西周时代的青铜器上有复杂的纹饰，这些纹饰或与贵族的祖先、神灵崇拜有关，或与他们的权力、财产有关。有的青铜器上还刻有文字、纪念祖先、记录赏赐或王命。依据以上内容，谈谈你对青铜器的综合认识。