问题
单项选择题
函数
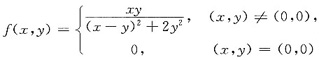在点(0，0)处
(A) 连续，但偏导数f’x与f’y不存在．
(B) 既不连续，偏导数f’x与f’y也不存在．
(C) 两个偏导数f’x与f’y都存在，但函数f(x，y)不连续．
(D) 可微分．
答案
参考答案：C
解析： 当x=y≠0时
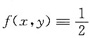，这表明在点(0，0)的任意小的邻域中总有使
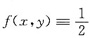的点，而f(0，0)=0，故f(x，y)在点(0，0)处不连续．
又因
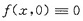可见f’x(0，0)=0，类似又有
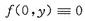，于是f’y(0，0)=0，这表明f(x，y)在点(0，0)处两个偏导数都存在．故应选(C)．