问题
填空题
差分方程yt+1-2yt=
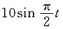 的通解是______.
的通解是______.
答案
参考答案:
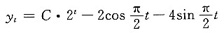
解析: 由于一阶常系数线性差分方程yt+1+ayt=f(t)的通解具有形式yt=C(-a)t+y*t,其中C是任意常数,而y*t是该方程的一个特解,它的形式由系数a的取值与方程右端项f(t)的形式所决定,在题设的方程中系数a=-2,方程右端项
 ,从而可设方程的通解为
,从而可设方程的通解为
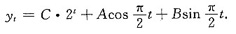
代入方程知待定常数A、B应满足关于t的恒等式

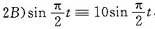 ,即
,即
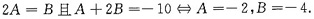 故方程的通解是
故方程的通解是

[注意] 当f(t)是多项式,指数函数,正弦函数,余弦函数以及它们的和差或乘积时,常用待定系数法求非齐次线性差分方程yt+1+ayt=f(t)的一个特解,与二阶常系数线性微分方程类似,可分为两大类来讨论.
若f(t)=Pm(t)dt,其中Pm(t)是t的m次多项式,常数d≠0.当非齐次项f(t)=Pm(t)时可看成d=1的特例.
特解的取法如下表:(其中Qm(t)是待定系数的m次多项式)

若f(t)=Mcosωt+Nsinωt,其中M,N,ω是常数,且0<ω<2π,ω≠π.这时总可以取函数y*t=Acosωt+Bsinωt为非齐次方程的一个特解,其中A,B是待定常数.
