设f(x)在[0,+∞)连续,在(0,+∞)可导,x∈(0,+∞)时f(x)>0且单调上升,x=g(y)为y=f(x)的反函数,它们满足
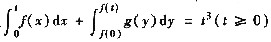 ,则f(x)的表达式是______.
,则f(x)的表达式是______.
参考答案:f(x)=x2(x≥0)
解析:[分析一] 由定积分的几何意义知:
[*]=由曲线y=f(x),x、y轴及直线x=t>0所围成的曲边梯形的面积,
[*]=由曲线x=g(y),y轴(y≥f(0))及直线y=f(t)所围成的曲边三角形的面积.
x=g(y)与y=f(x)互为反函数,代表同一条曲线,它们面积之和是长方形面积(边长分别为t与f(t)),见右图.
[*]
于是 [*]
因此tf(t)=t3,f(t)=t2(t≥0),
即 f(x)=x2(x≥0).
[分析二] 先化简题设方程的左端式子,有
[*]
于是 [*]
即 tf(t)=t3,f(t)=t2(t≥0).
因此 f(x)=x2(x≥0).
[分析三] 将题设方程两边求导得
[*]
即 f(t)+g[f(t)]f’(t)=3t2,
f(t)+tf’(t)=3t2,
亦即 [tf(t)]’=3t2
(原方程中令t=0,等式自然成立,不必另加条件).将上式积分得
tf(t)=t3+C,即[*].
因f(t)在[0,+∞)连续,故必有C=0.
因此f(x)=x2(x≥0).
