问题
问答题
设函数f(x)在点x=0处三阶可导，且满足
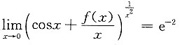求f(0)，f’(0)，f"(0)与f"’(0)．
答案
参考答案：[解] 利用当g(x)→0时ln[1+g(x)]～g(x)可得
把f(x)的带皮亚诺余项的三阶麦克劳林公式f(x)=f(0)+f’(0)x2+
代入即得
(*)式可改写成为
不难发现只要f(0)，f’(0)，f"(0)之一不是零，上式就不可能成立，
故f(0)=f’(0)=f"(0)=0，而f"’(0)=-9．