参考答案：

[分析]： 若p(x)在[0，1]上连续．在(0，1)内可导且在(0，1)内不等于零，于是

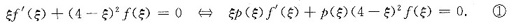
若[xp(x)]’=p(x)(4-x)²，则①式可改写成

令F(x)=xp(x)f(x)，可见F(x)在[0，1]上连续，在(0，1)内可导且F(0)=0，又由f(0)f(1)＜0及f(x)在[0，1]上连续可知，存在η(0，1)使得f(η)=0，从而F(x)在[0，η]上满足罗尔定理的全部条件．由罗尔定理知：

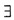ζ∈(0，η)

(0，
1)使得F’(ζ)=0，即题目的结论成立．

从而

[证明]由f(x)在[0，1]上连续且f(0)f(1)＜0知

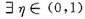使得f(η)=0．
设

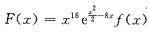，由题设知F(x)在[0，η]上连续，在(0，η)内可导，且F(0)=F(η)．按罗尔定理知：存在ζ∈(0，η)即ζ∈(0，1)使得F’(ζ)=0．由于

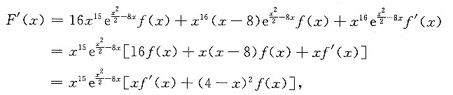
且

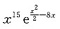在(0，η)内不等于零，故由F’(ζ)=0即知

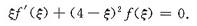
证毕．