问题
问答题
设
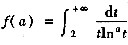 ,试求:
,试求:
(Ⅰ) 函数f(a)的定义域;(Ⅱ) 函数f(a)的值域.
答案
参考答案:(Ⅰ) 即求a的取值范围,使得该无穷积分收敛.
当a≠1时,
[*]
当a=1时,
[*]
因此,仅当a>1时原积分收敛,即函数f(a)的定义域是(1,+∞).
(Ⅱ) 为求[*]在(1,+∞)上的值域,先考察
[*]
求值域归结为求f(a)的最小值.求f(a)在(1,+∞)的最小值等价于求g(a)=(a-1)lna-12
在(1,+∞)的最大值.由
g’(a)=lna-12+(a-1)lna-12·lnln2=lna-12[1+(a-1)lnln2]
=[*]
[*]g(a)在a=a0处取最大值[*]f(a)的最小值为
[*]
因此f(a)的值域是[a*,+∞).
