阅读理解。
That little "a" with a circle around it is most commonly used as the "at" symbol. The symbol is usually
found in e-mail addresses. Surprisingly though, there is no official (官方的) name for this symbol, there
are lots of strange ways to describe the @ symbol. Before the @ symbol became the popular symbol for e-mail, it was used to show the cost of something. For example, if you bought 6 apples, you might write
6 apples @$1.10 each.
As e-mail is becoming more and more popular, the@symbol or the"at sign is used between a person's
online user name and his mail server address, for example, joe@126.com. The symbol's use on the
Internet made it necessary for people to put this symbol on keyboards in the countries that had never seen or used the symbol before.
The actual origin (起源) of the @ symbol remains a mystery. According to an ancient western legend, during the Middle Ages before the invention of the printing press (印刷机), every letter of a word had
to be written by hand for each copy of a book. The monks (僧侣) looked for ways to make the letters
of common words less. Although the word "at" was quite short, it was quite a common word in texts and
documents. As a result, they circled around "a" and created @.
根据短文内容,选择最佳选项。
1. What did someone mean by writing 5 pears @$2.0 each in the past?
A. He bought 5 pears for free.
B. He paid $7.0.
C. 5 pears cost $2.0.
D. Each pear was $2.0.
2. Why did the monks in the old times create @ most probably?
A. Because @ could be printed very easily and clearly.
B. Because they were ordered to invent some symbols.
C. Because they didn’t want to write the word "at" again and again.
D. Because they wanted to make their texts or documents look special.
3. Which of the following is NOT true?
A. @ is often seen in e-mail addresses today.
B. The @ symbol has always meant the same in history.
C. The Internet makes @ become more popular.
D. The actual origin of @ is still difficult to explain.
4. What do we know from the passage?
A. @ was used before the Middle Ages.
B. @ is still always used to show prices of goods now.
C. No one had seen @ before it was put on the keyboard.
D. There was no @ on keyboards in some countries before.
5. Which is the BEST title for the passage?
A. What is @
B. The secret of @
C. How to use @
D. The actual origin of @
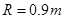 的四分之一光滑圆弧轨道
的四分之一光滑圆弧轨道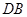 固定在竖直面内,最低点
固定在竖直面内,最低点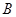 与长
与长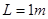 的水平轨道相切于
的水平轨道相切于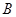 点。
点。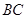 离地面高
离地面高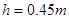 ,
,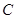 点与一倾角为
点与一倾角为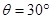 的光滑斜面连接。质量
的光滑斜面连接。质量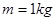 的小滑块从圆弧顶点
的小滑块从圆弧顶点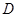 由静止释放,滑块与BC间的动摩擦因数
由静止释放,滑块与BC间的动摩擦因数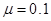 。取
。取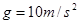 。求:(1)小滑块刚到达圆弧的
。求:(1)小滑块刚到达圆弧的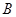 点时对圆弧的压力;(2)小滑块到达
点时对圆弧的压力;(2)小滑块到达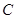 点时的速度大小;(3)小滑块从
点时的速度大小;(3)小滑块从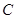 点运动到水平面所需的时间。
点运动到水平面所需的时间。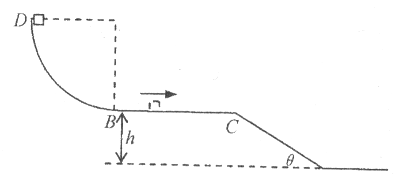
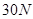 ,向下 (2)
,向下 (2)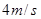 (3)
(3)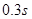
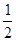 mvB2
mvB2 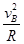 ,联立 上式解得:F=30N ,压力方向向下
,联立 上式解得:F=30N ,压力方向向下 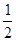 mvC2
mvC2 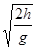 =1.2m ,
=1.2m , 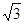 m , 因为S>d,所以小滑块离开C点将落在水平地面上,小滑块在空中的飞行时间即为小滑块平抛运动所用时间t=
m , 因为S>d,所以小滑块离开C点将落在水平地面上,小滑块在空中的飞行时间即为小滑块平抛运动所用时间t=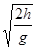 =0.3s
=0.3s 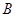 点时对圆弧的压力大小为30N,方向向下;
点时对圆弧的压力大小为30N,方向向下;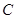 点时的速度大小为4 m/s
点时的速度大小为4 m/s 点运动到水平面所需的时间0.3s.
点运动到水平面所需的时间0.3s.